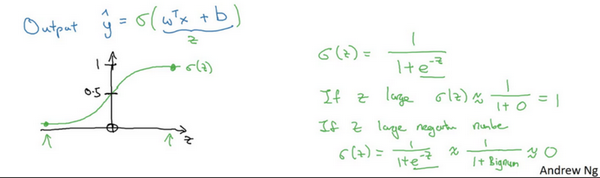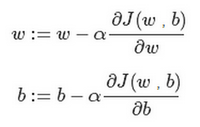logistics
==二元分类==
输出:标签1/0
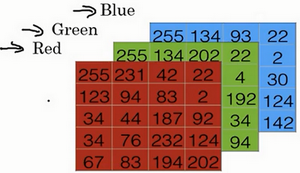
img在计算机中保存–>三个矩阵(假设64*64,那么就有3 * 64 * 64个像素,变成特征向量,总维度,也就是矩阵的行为n=3 * 64 * 64,如果有m组训练集,那么矩阵最终为m列,n行)
==logistics回归==
y^ 表示 y 等于1的一种可能性或者是机会
w 表示逻辑回归的参数,这也是一个 n 维向量(因为 w 实际上是特征权重,维度与特征向量相同),参数里面还有 b,这是一个实数(表示偏差)
选择使用sigmoid函数原因:如果单纯线性,无法把y^值控制在0-1之间,故取sigmoid(z)
使得z很大,sigmoid(z)趋近1, z 变成一个绝对值很大的负数,sigmoid(z)趋近0
==损失函数==
$L(\hat{y},y) = -y\log(\hat{y})-(1-y)\log(1-\hat{y})$ 单次
成本(代价)函数:$J(w,b) = \frac{1}{m}\sum_{i=1}^{m}{(-y\log(\hat{y})-(1-y)\log(1-\hat{y}))}$ 也就是总代价,训练逻辑回归模型时候,我们需要找到合适的 w 和 b ,来让代价函数 J 的总代价降到最低
==梯度下降法==
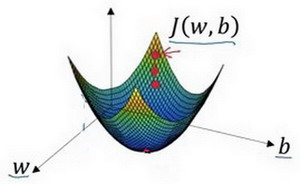
J 为凸函数,没有局部最优,只有全局最优
朝最陡的下坡方向走一步,不断地迭代
更新w,b 找到最合适的参数使得J = Jmin
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Eason-hk-barcelona!
评论